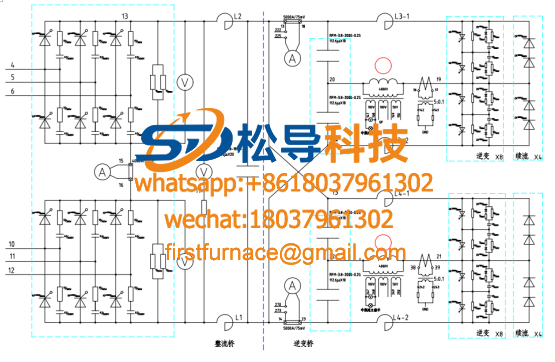
Summary of technical parameters of 10 ton induction melting furnace_Energy saving induction heating equipment manufacturers

The 10- ton one-to-two induction melting furnace consists of a high-voltage switchgear, a rectifier transformer, a 12- pulse intermediate frequency power supply, and two 10- ton furnace bodies (with and without furnace cover). there are both manual and hydraulic operation), a hydraulic device (a dual pump hydraulic system, the hydraulic cylinders tilting furnace . 4 rats lining the top of the cylinder 1 rats), a station console tilting furnace, water dispenser, water cooling , A set of intermediate frequency power supply respectively supplies power to two electric furnaces. Two furnaces can be smelted at the same time, or one induction melting furnace can be smelted, and the other induction melting furnace can control the required temperature for casting or heat preservation. (Called one to two 10 tons induction melting furnace ).

10 ton one-to-two induction melting furnace : It has protection systems such as overvoltage, overcurrent, furnace lining, water temperature, water pressure, short circuit, and grounding, and has fault, temperature and other indications.

Main technical parameters of 10 ton one to two induction melting furnace

project	unit	data
Electric furnace parameters	T	10t
Rated Capacity	t	10
Z large capacity	t	11
Induction coil inner diameter φ	mm	1200
Induction coil height	mm	2050
Z high working temperature	°C	1800
Transformer capacity	KVA	8000
Transformer primary voltage	KV	10
Transformer secondary voltage	V	950
Rated power of intermediate frequency power supply	KW	8000kw smelting furnace power 6500kw, holding furnace 1500kw, power adjustable
Coil voltage	V	3000
Rated working frequency	Hz	300
Power conversion efficiency	%	96
Startup success rate	%	100
Comprehensive parameters
Equipment power factor		≥0.96
Melting rate (heating up to 1800 ℃)	t/h	12
Melting power consumption (heating up to 1800 ℃)	KW.h/t	550
Working noise	db	≤75
Hydraulic system
Hydraulic station capacity	L	800
Work pressure	MPa	15
Hydraulic medium		Hydraulic oil
Cooling water system
flow	M3/h	120
Water supply pressure	MPa	0.2～0.3
Inlet water temperature	°C	5～35
Outlet temperature	°C	35～55
Leaking furnace alarm device	2 sets
price

Common parallel lines old model 10 tons induction melting furnace by the power of 6000 kW of frequency power supply 1 set with 10 tons two melting furnace. Use two 3150KVA special rectifier transformers to form a 12- pulse 6000KW intermediate frequency power supply.

Serial number	Term project	Reference number	Preparation Note
1	Power incoming line voltage	950V , 50Hz	User grid voltage 35KV
2	Rated Capacity	10T	6000KW power melting and heat preservation
3	rated power	6000KW	6-phase 12-pulse control system
4	Rated intermediate frequency	350 Hz
5	Rated temperature	1700°C
6	Melting rate	About 8T/H	Continuous use of melting furnace
7	Unit power consumption	Melting about 550-600kwh/T	Continuous use of melting furnace
8	Power cooling circulating water consumption	35T/H	Continuous use of melting furnace
8	Circulating water consumption of furnace cooling	30T/H	Continuous use of melting furnace
9	Hydraulic station capacity	200 L
10	Transformer model	ZSS -3150 /10KV/950x2	Dedicated rectifier transformer (for 6000KW)
11	Hydraulic medium	No. 46 hydraulic oil
12	Water supply pressure	0.2-0.3 MPa	To the position of the electric furnace port
13	Working pressure of hydraulic station	15 MPa	Z height 18 MPa
14	Inlet water temperature	£35℃
15	Outlet temperature	£55℃